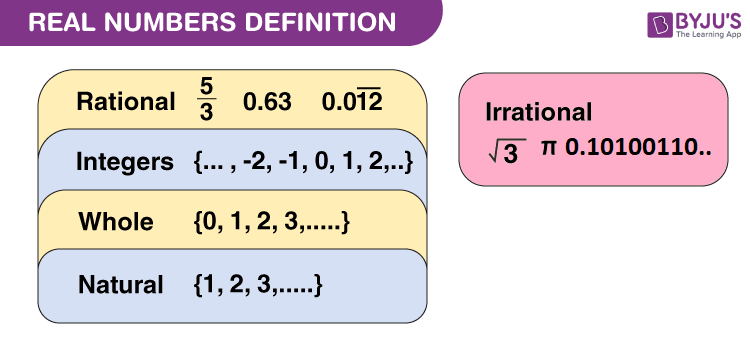
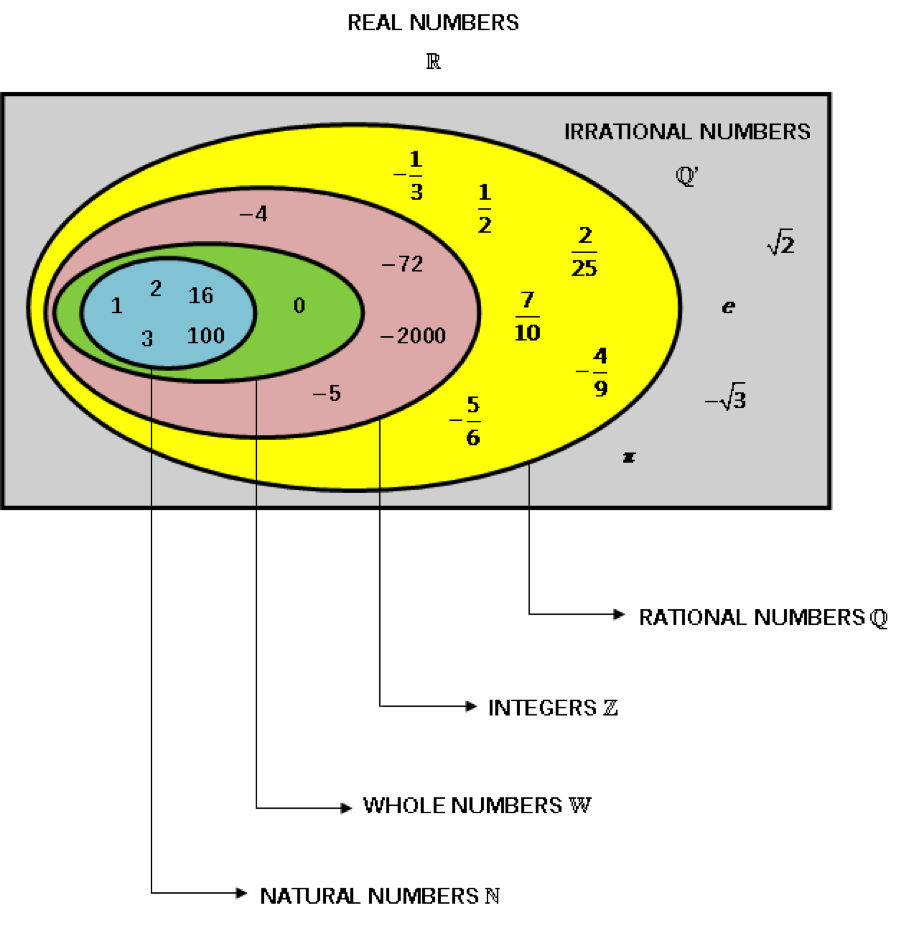
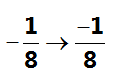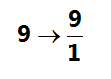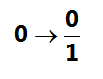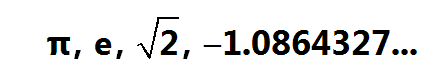Real Numbers- Definition, Properties and more

Real Numbers Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also. At the same time, the imaginary numbers are the un-real numbers, which cannot be expressed in the number line and is commonly used to represent a complex number. The concepts related to real numerals are explained here in detail, along with examples and practice questions. The key concept in the number system is included in this article. Real Numbers Definition Real numbers can be defined as the union of both the rational and irrational numbers. They can be both positive or negative and are denoted by the symbol “R”. All the natural numbers, decimals and fractions come under this category. See the figure, given below, which shows the classification of real numerals.

The set of real numbers consist of different categories, such as natural and whole numbers, integers, rational and irrational numbers. In the table given below, all these numbers are defined with examples.

Category	Definition	Example
Natural Numbers	Contain all counting numbers which start from 1. N = {1,2,3,4,……}	All numbers such as 1, 2, 3, 4,5,6,…..…
Whole Numbers	Collection of zero and natural number. W = {0,1,2,3,…..}	All numbers including 0 such as 0, 1, 2, 3, 4,5,6,…..…
Integers	The collective result of whole numbers and negative of all natural numbers.	Includes: -infinity (-∞),……..-4, -3, -2, -1, 0, 1, 2, 3, 4, ……+infinity (+∞)
Rational Numbers	Numbers that can be written in the form of p/q, where q≠0.	Examples of rational numbers are ½, 5/4 and 12/6 etc.
Irrational Numbers	All the numbers which are not rational and cannot be written in the form of p/q.	Irrational numbers are non-terminating and non-repeating in nature like √2

Real Number System

A real number is a number that can be found on the number line. These are the numbers that we normally use and apply in real-world applications.

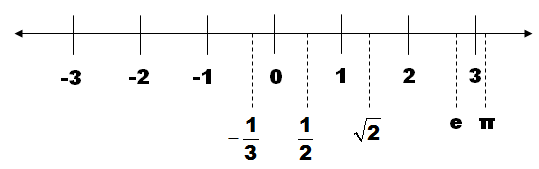
There are many types of real numbers. Here are some of them:-

Natural numbers Whole numbers  Integers  Fractions  Rational numbers  Irrational numbers

 

Below is a diagram of the real number system.

Real numbers are mainly classified into rational and irrational numbers. Rational numbers include all integers and fractions. All negative integers and whole numbers make up the set of integers. Whole numbers comprise of all natural numbers and zero.

 

 

 

Natural Numbers

A natural number is a counting number. It starts from 1 onwards. They are located at the right side of the number line (after 0).

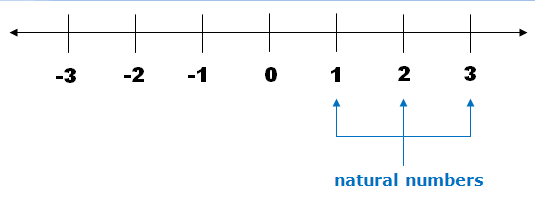
1 Is The Smallest Natural Number.

Examples of natural numbers are 1, 2, 3, 4, 5, 10, 68, 101, 422, 1024   Which of the following is/are natural numbers? −1,0,14,50000,3.7-1,0,14,50000,3.7 Answer: −1,0-1,0, and are not natural numbers since they are less than 11. 3.73.7 is not a natural number since you cannot count it. 5000050000 is a natural number since you can count it. Therefore, the natural number is 5000050000.

 

 

Whole numbers

A whole number is either a counting number or zero (0). They are located at the right side of the number line.

0 Is The Smallest Whole Number.

Eamples of whole numbers are 0, 1, 2, 3, 16, 78, 904, 1556, 38617   Which of the following is/are whole numbers? 16,−4,15,0,0.0316,-4,15,0,0.03 Answer: −4-4 is not a whole number since it is less than 00. 0.030.03 and 1515 are not whole numbers since you cannot count them. 00 and 1616 are whole numbers since you can count them. Therefore, the whole numbers are 00 and 1616.

 

 

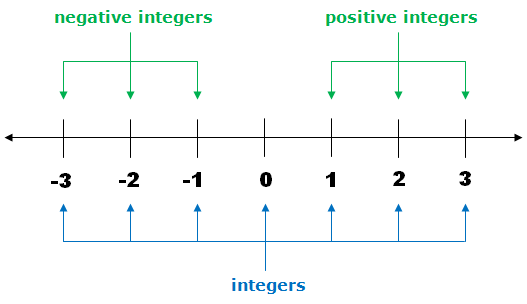
Integers

An integer is either a whole number or its negative. Positive integers are integers starting from 1 and so on. They are located at the right side of the number line (after 0). They are also natural or counting numbers.   Negative integers are integers starting from -1 and so on. They are located at the left side of the number line (before 0). They are negative whole numbers.   Examples of integers are -2015, -197, -44, -3, 0, 6, 28, 143 Which of the following is/are integers? −31,−23,0.7,0,46-31,-23,0.7,0,46 Answer: -2323 is not an integer since it is not a whole number 0.7 is not an integer since it is not a whole number. -31 is an integer since it is a negative whole number. 0 is an integer since it is a whole number. 46 is an integer since it is a whole number.

 

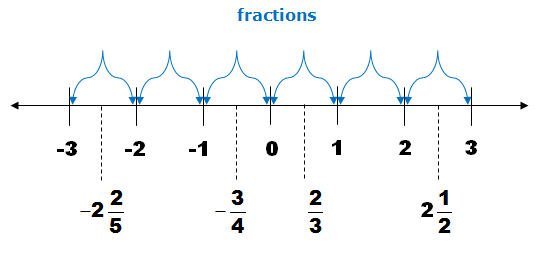
Fractions

A fraction is a part of a whole. In the number line, they are located between integers.   Examples of fractions are -3 1414 , -2525 , -110110 ,920920 ,1616 ,5 1212 A fraction can be converted into decimal form.   Which of the following is/are fractions? −6-6,−115-115 , −37-37, 2.14,02.14,0, 2929 Answer: −6-6 is not a fraction since it is a negative whole number. 00 is not a fraction since it is a whole number. −115-115 , −37-37and 2929 are fractions since they are parts of a whole. 2.142.14 is a fraction. Why? Because it is between two integers (22 and 33) and it is a part of a whole since 2.142.14 = 214100214100 or 27502750 . Therefore, the fractions are −115-115 , −37-37, 2.142.14, 29

 

Rational Numbers

A rational number is a number that can be written as a ratio of two integers. It can be a fraction, an integer, a whole number, or even a natural number. Examples of rational numbers are −523,−18,−4,0,37,9-523,-18,-4,0,37,9 In the example, −18-18 is a rational number since it can be a ratio of integers -1 and 8.   99 is a rational number since it can be a ratio of integers and 1.   00 is a rational number since it can be a ratio of integers 0 and 1.   For decimal numbers, it can be a rational number if it satisfies either one of the following:    It has finite number of digits.      Its digits are repeating in a continuous manner. 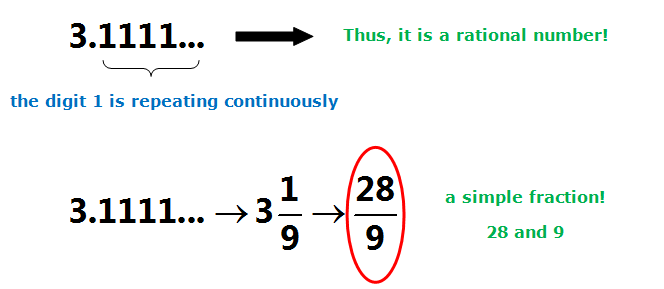Which of the following decimals is/are rational numbers? (a) -1.232323… (b) 3.141592653… (c) 0.123456789 Answer: (a) -1.232323… The digits 2 and 3 are repeating continuously. Thus, it is a rational number. (b) 3.141592653… It has an infinite number of digits and there are no repeating digit patterns. Thus, it is not a rational number. (c) 0.123456789 It has a finite number of digits, which is 10. Thus, it is a rational number. Therefore, the rational numbers are -1.232323… and 0.123456789.

 

 

Irrational Numbers

An irrational number is a number that cannot be written as a ratio of two integers. It is a non-terminating and non-repeating decimal. Examples of irrational numbers are   In the example,   π is an irrational number since it cannot be written as a ratio of two integers.   0 is an irrational number since it cannot be written as a ratio of two integers.   2–√2 is an irrational number since it cannot be written as a ratio of two integers.     Which of the following decimals is/are irrational numbers? (a) 6.71842013…6.71842013… (b) 2.193746612.19374661 (c) 3–√3 (d) −4–√-4 Answer: (a)6.71842013…(a)6.71842013… The decimal has an infinite number of digits and no digit pattern. Thus, it is an irrational number.   (b)2.19374661(b)2.19374661 Even though the decimal has no digit pattern, it has a fixed number of digits.Thus, it is not anirrational number. (c) 3–√3 3–√3= 1.732050801.73205080 The decimal has an infinite number of digits and has no digit pattern.Thus, it is an irrational number. (d) −4–√-4 4–√=24=2 It is a whole number. Thus, it is not an irrational number. Therefore, the irrational numbers are 6.71842013…6.71842013… and 1.732050801.73205080.

 

Other Types Of Real Numbers Besides the main types of real numbers discussed earlier, these numbers can also be classified according to their properties and representation. Here are some: Positive And Negative Numbers Positive numbers are numbers that are greater than zero. Examples of positive numbers are 12,98455,1,0.1673...,5–√12,98455,1,0.1673...,5 Negative numbers are numbers that are less than zero. 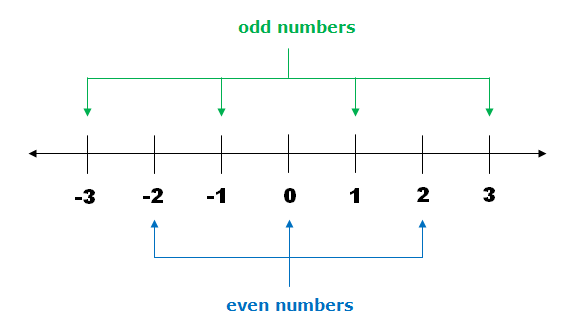−3,−7–√,−0.45612,−15,−19-3,-7,-0.45612,-15,-19   Even And Odd Numbers Even numbers are integers that are divisible by 2. They end with digits 0, 2, 4, 6, or 8. Examples of even numbers are 2,4,6,100,−8,−202,4,6,100,-8,-20 Odd numbers are integers that are not divisible by 2. They end with digits 1, 3, 5, 7, or 9. Examples of odd numbers are 1,5,3,99,−7,−411,5,3,99,-7,-41 In the number line, odd and even numbers are arranged alternately one after another. 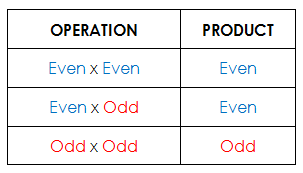Here are the results when adding (or subtracting) odd or even numbers: Same result if the operation is subtraction (-). The result is an even number if the numbers added are both even or both odd numbers. Otherwise, the result is an odd number. Here are the results when multiplying odd or even numbers: The result is an even number if one number being multiplied is an even number. Otherwise, the result is an odd number.   Prime And Composite Numbers Prime numbers are natural numbers whose factors are only itself and 1. 2 is the only prime number that is an even number. It is also the smallest prime number. Examples of prime numbers are 2,3,5,7,11,13,17,192,3,5,7,11,13,17,19 Composite numbers are natural numbers having at least one factor other than itself and 1. 4 is the smallest composite number. Examples of composite numbers are 4,6,8,9,10,38,250,17004,6,8,9,10,38,250,1700 The table below shows the prime and composite numbers from 1 to 100. *Prime numbers – Blue Squares *Composite numbers – White Squares *1 is neither a prime nor a composite number.   Identify what kind of number (positive, negative, even, odd, prime, composite) are the following: (a) 2323 (b) −7–√-7 (c) 00 (d) −59-59 (e) 11 Answer: (a)23(a)23 It is greater than 00 and has no sign. So it is a positive number. It ends with the digit 33 so it is an odd number. Its factors are 11 and itself so it is a prime number.   (b)7–√(b)7 It is less than 00 and has a negative sign (-). So it is a negative number. It is not an integer so it is neither an odd nor an even number. It is not a natural number so it is neither a prime nor a composite number.   (c)0(c)0 It is neither a positive nor a negative number. It ends with the digit 00 so it is an even number. It is not a natural number so it is neither a prime nor a composite number.   (d)−59(d)-59 It is less than 00 and has a negative sign (-) so it is a negative number. It ends with the digit 99 so it is an odd number. It is not a natural number so it is neither a prime nor a composite number.   (e)1(e)1 It is greater than 00 and has a no sign so it is a positive number. It ends with the digit 1 so it is an odd number. 22 is the smallest prime number while 44 is the smallest composite number so it is neither a prime nor a composite number.   Tricks To Remember While Solving Number System Questions:- 1 is neither divisible nor prime. Two consecutive odd prime numbers are known as prime pair. All natural numbers are whole, integer, rational and real. All whole numbers are rational, Integer and real. All rational numbers incorporates integers, since every integer can be written as a fraction with denominator 1. Example (9/1). The square of an even is even and the square of an odd number is odd. Any given Prime Number can never be a Composite Number. Fractions are rational. Zero is neither negative nor positive number. If x is any number then, if x divides zero, result will be zero. If 0 divides x, then result will be infinite or not defined or undetermined i.e. 0/x =0, but x/0 =∞ (infinite) where x is real number. The sum and the product of two rational number is always a rational numbers. The product or the sum of a rational number and irrational number is always an irrational number.